Un rettangolo avente il perimetro di 140 cm e l'altezza che misura 3/4 della base è inscritto in un cerchio. Calcola la differenza tra l'area del cerchio e l'area del rettangolo
Ricompensa per la miglior risposta: 10 monete 
Per risolvere il problema fai riferimento alla seguente figura
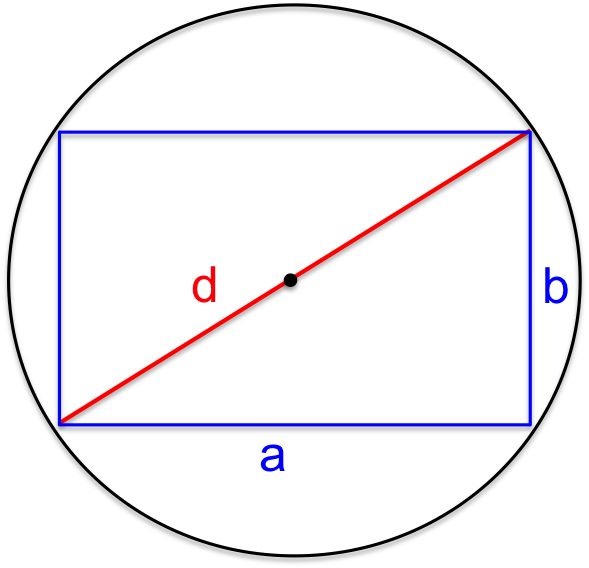
DATI DEL PROBLEMA:
\(P = 140 \text{ cm}\);
\(b = \dfrac{3}{4} a\);
SVOLGIMENTO
La somma dei lati \(a\) e \(b\) è uguale a metà perimetro
\(a + b = \dfrac{P}{2} = \dfrac{140}{2} = 70;\)
Poichè sappiamo che
\(b = \dfrac{3}{4} a\)
possiamo sostituire \(b\) nella formula del semiperimetro e calcolare \(a\):
\(a + \dfrac{3}{4} a = 70; \)
\(\dfrac{3 + 4}{4} a = 70; \)
\(\dfrac{7}{4} a = 70;\)
\(a = \dfrac{70}{7} \cdot 4 = 40\)
A questo punto possiamo calcolare b, sostituendo il valore di a nella formula del semiperimetro:
\(40 + b = 70 \)
\(b = 70 - 40\)
Applicando il teorema di Pitagora calcoliamo il diametro:
\(d = \sqrt{a^2 + b^2}\)
il raggio è uguale al diametro diviso 2:
\(r = \dfrac{d}{2} = 25\)
Calcolo AREA DEL CERCHIO
\(Ac = 3.14 \cdot r^2 = 3.14 \cdot 625 \text{ cm^2}\)
Calcolo AREA DEL RETTANGOLO
\(Ar = a \cdot b = 30 \cdot 40 = 1200 \text{ cm^2}\)
Calcolo differenza tra area cerchio e quella del rettangolo
\(D = Ac - Ar = 762,5 \text{ cm^2}\)