in un trapezio rettangolo la diagonale minore forma con la base maggiore un angolo di 60° ed è perpendicolare al lato obliquo.Calcola l'ampiezza degli angoli del trapezio
Ricompensa per la miglior risposta: 1 moneta 
La soluzione al tuo problema è molto semplice, basta far riferimento alla figura sottostante.
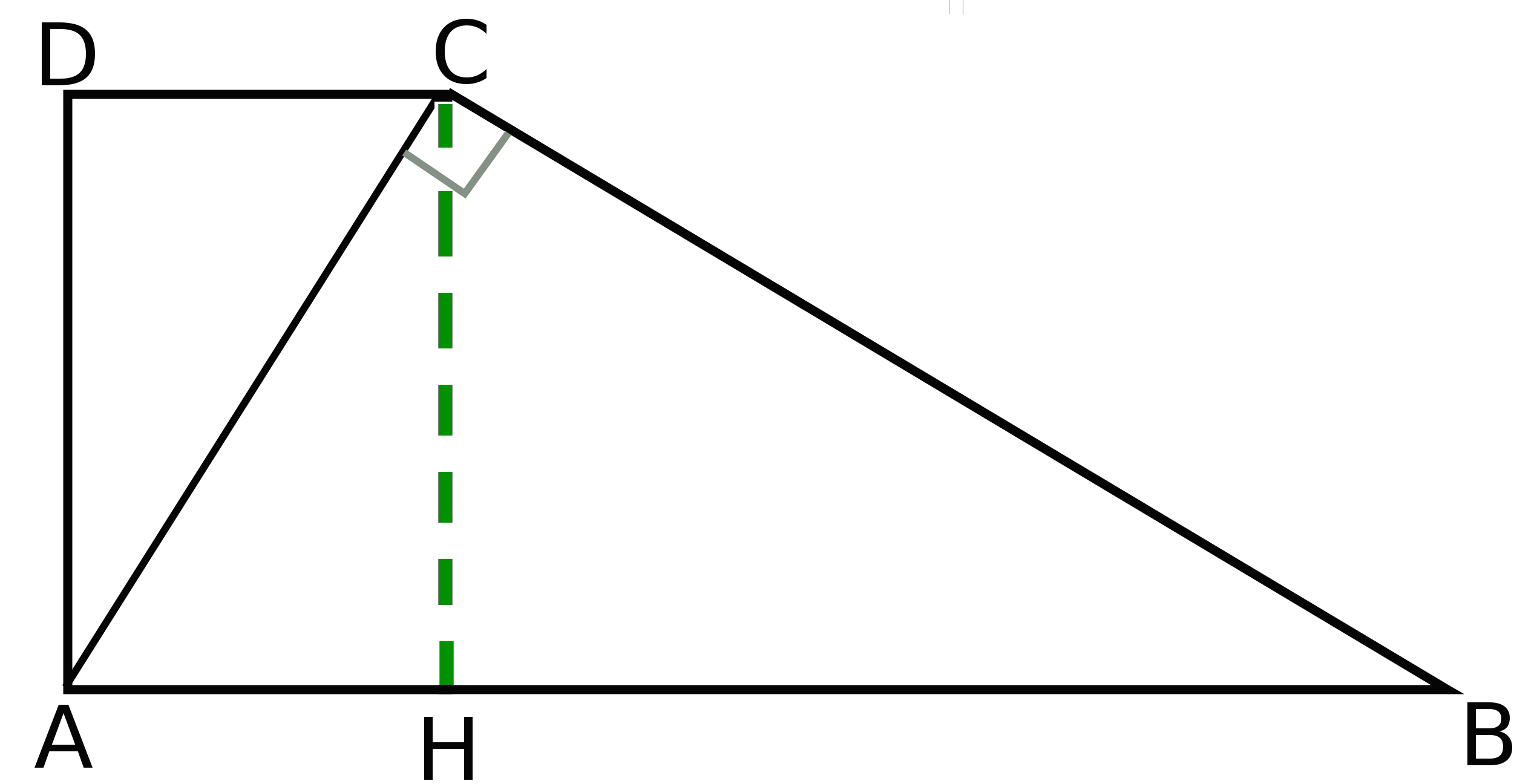
Nel trapezio rettangolo mostrato in figura la diagonale minore è AC che forma un angolo di 60° con la base maggiore AB, quindi:
\(\hat{CAB} = 60°\)
Poichè AC è perpendicolare al lato obliquo CB, l'angolo formato è di 90°, cioè:
\(\hat{ACB} = 90°\)
Poichè in un triangolo la somma degli angoli è di 180° possiamo calcolare l'angolo tra il lato obliquo e la base maggiore:
\(\hat{CBA} = 180° - (\hat{CAB} + \hat{ACB}) = 180° - (60° + 90°) = 30°\)
L'altezza AD forma un angolo di 90° con la base maggiore AB e con la base minore DC perchè si tratta di un trapezio rettangolo, quindi:
\(\hat{DAB} = 90°\)
\(\hat{ADC} = 90°\)
Poichè la somma degli angoli interni di una quadrilatero è uguale a 360°, si ha che:
\(\hat{DCB} = 360° - (\hat{DAB} + \hat{ADC} + \hat{CBA}) = 360° - (90° + 90° + 30°) = 150°\)
Abbiamo così calcolato tutti gli angoli del quadrilatero.