Scrivo i dati del problema facendo riferimento alla seguente figura:
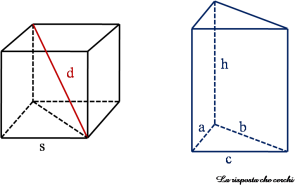
- \(a = 7 \text{ cm}\) (cateto minore della base del prisma );
- \(b = 24 \text{ cm}\) (cateto maggiore della base del prisma );
- \(h = \dfrac{9}{4} P_{triangolo}\) (altezza prisma è 9/4 del perimetro di base);
- \(S_{cubo} = S_{prisma}\) (superficie laterale cubo è uguale a quella del prisma);
Di seguito è riportata la procedura per calcolare lo spigolo del cubo \(\left(s\right)\) e la sua diagonale \(\left(d\right)\).
CALCOLO IPOTENUSA della base del prisma
Utilizzo la lettera \(c\) per indicare l'ipotenusa della base del prisma. Applicando il teorema di Pitagora (il quadrato dell'ipotenusa è uguale alla somma dei quadrati dei cateti), si ha:
\(c = \sqrt{a^2 + b^2} = \sqrt{\left(7^2 + 24^2\right)\text{ cm}^2} = \sqrt{625\text{ cm}^2)} = 25\text{ cm}\);
CALCOLO PERIMETRO della base del prisma
Indico con \(P_{triangolo} \) il perimetro della base del prisma:
\(P_{triangolo} = a + b + c = (7+ 24 + 25)\text{ cm} = 56\text{ cm}.\)
CALCOLO ALTEZZA del prisma
Per calcolare l'altezza \(h\) del prisma utilizziamo il dato 3 del problema:
\(h =\dfrac{9}{4} P_{triangolo} = \dfrac{9}{4} 56\text{ cm} = 126\text{ cm}\).
CALCOLO SUPERFICIE LATERALE prisma
Ricordando che la superficie laterale di un prisma si calcola moltiplicando il perimetro della base per l'altezza del prisma, si ha:
\( S_{prisma} = P_{prisma}\cdot h = \left(56\cdot 126\right)\text{ cm}^2 = 7056\text{ cm}^2\).
CALCOLO SPIGOLO del cubo
Dalla traccia del problema sappiamo che la superficie laterale del cubo è equivalente a quella del prisma, quindi:
\( S_{cubo} =S_{prisma} = 7056\text{ cm}^2\).
La superficie laterale di un cubo si ottiene sommando 4 facce del cubo, che sono tutte uguali. Pertanto, l'area della base del cubo, che indichiamo con \( A_{c}\), si può calcolare dividendo la superficie laterale per 4:
\(A_{c} = \dfrac{S_{prisma}}{4} = \dfrac{7056\text{ cm}^2}{4} = 1764\text{ cm}^2\).
Conoscendo l'area di base del cubo, lo spigolo si può calcolare facilmente facendo la radice quadrata dell'area:
\( s = \sqrt{A_{c}} = \sqrt{1764\text{ cm}^2} = 42\text{ cm}\).
CALCOLO DIAGONALE del cubo
La diagonale di un cubo si calcola moltiplicando lo spigolo di base per \(\sqrt{3}\):
\( d = s\cdot \sqrt{3} = 42\cdot \sqrt{3}\text{ cm} = 72,7461\).
CONCLUSIONE
Lo spigolo del cubo è uguale a \(42\text{ cm}\), mentre la sua diagonale è uguale a circa \(72,7461\text{ cm}\).
