Problema parallelogramma - calcolo diagonale maggiore
Un parallelogramma è formato da due triangoli rettangoli di cateti lunghi 5 cm e 10 cm e da un rettangolo di lati 10cm e 15 cm. Quanto misura la diagonale maggiore?
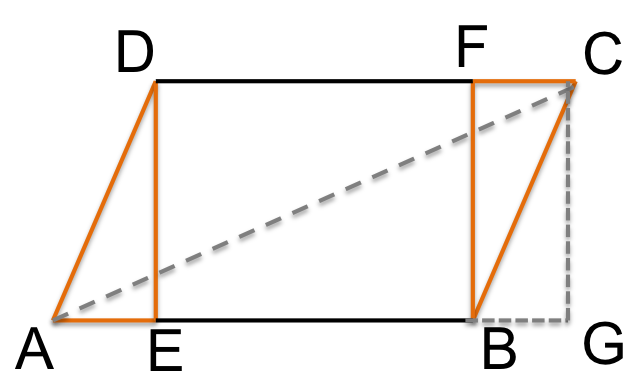
Figura 1: Parallelogramma
Si faccia riferimento alla Figura 1
Il Problema del parallelogramma richiede di trovare la diagonale maggiore del parallelogramma, ossia AC
AC = ?
I dati del problema sono:
AE = FC = 5 cm
DE = BF = 10 cm
DF = EB = 15 cm
Tenendo conto dei dati e della Figura 1 si ha che
AB = AE + EB = 20 cm
DC = AB = 20 cm
Si consideri il triangolo AED, per il Teorema di Pitagora, l’ipotenusa AD è:
\(AD = \sqrt{AE^2+DE^2} = \sqrt{25+100} = \sqrt{125} = 11.18\)
Si consideri ora, il triangolo ACG:
CG = DE = 10 cm
BG = FC = 5 cm
AG = AB + BG = 20 cm + 5 cm = 25 cm
Per il Teorema di Pitagora, , l’ipotenusa AC, che è anche la DIAGONALE MAGGIORE del Parallelogramma è
\(AC = \sqrt{AG^2+CG^2} = \sqrt{625+100} = \sqrt{725} = 26.92\)